Heat ball
by Willie Wong
There are very few things I find unsatisfactory in L.C. Evans’ wonderful textbook on Partial Differential Equations; one of them is the illustration (on p.53 of the second edition) of the “heat ball”.
The heat ball is a region with respect to which an analogue of the mean value property of solutions to Laplace’s equation can be expressed, now for solutions of the heat equation. In the case of the Laplace’s equation, the regions are round balls. In the case of the heat equation, the regions are somewhat more complicated. They are defined by the expression
where is the fundamental solution of the heat equation
In the expressions above, the constant is the number of spatial dimensions;
is the analogue of the radius of the ball, and in
, the point
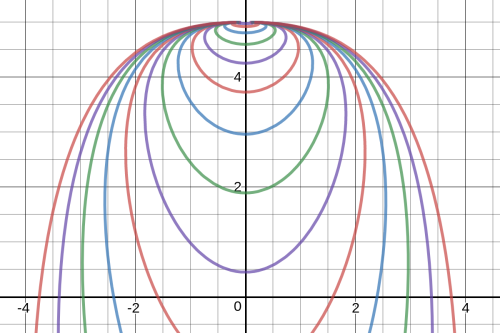
is the center. Below is a better visualization of the heat balls: the curves shown are the boundaries
in dimension
, for radii between 0.75 and 4 in steps of 0.25 (in particular all the red curves have integer radii). In higher dimensions the shape is generally the same, though they appear more “squashed” in the
direction.
Eventually, I saw a PDE professor points this out 🙂 I think Evans should certainly give a better picture than the one in his book.
A related answer in MSE: https://math.stackexchange.com/a/1169860/9464
Willie: What functions did you put into the Desmos to get the picture?
Desmos allows implicitly defined functions! So I just took the definition of the heat ball (exactly as displayed in Evans [equiv. as above], except using the variable y in place of t so that Desmos would recognize), replaced the inequality by an equals sign, and changed the radii and center to be concrete numbers.