It is generally well known that partial differential equations that model fluid motion can exhibit “shock waves”. In fact, the subject I will write about today is generally presented as the canonical example for such behaviour in a first course in partial differential equations (while also introducing the method of characteristics). The focus here, however, will not be so much on the formation of shocks, but on the profile of the shock boundary. This discussion tends to be omitted from introductory texts.
Solving Burgers’ equation
First we recall the inviscid Burgers’ equation, a fundamental partial differential equation in the study of fluids. The equation is written
Equation 1. Inviscid Burgers’ equation

where  is the “local fluid velocity” at time
is the “local fluid velocity” at time  and at spatial coordinate
and at spatial coordinate  . The solution of the equation is closely related to its derivation: notice that we can re-write the equation as
. The solution of the equation is closely related to its derivation: notice that we can re-write the equation as

The question we consider is the initial value problem for the PDE: given some initial velocity configuration 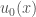 , we want to find a solution
, we want to find a solution  to Burgers’ equation such that
to Burgers’ equation such that 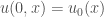 .
.
The traditional way of obtaining a solution is via the method of characteristics. We first observe (1) the alternate form of the equation above means that if  is a curve tangent to the vector field
is a curve tangent to the vector field  , we must have
, we must have 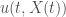 be a constant valued function of the parameter
be a constant valued function of the parameter  . (2) Plugging this back in implies that along such a curve
. (2) Plugging this back in implies that along such a curve  , the vector field
, the vector field  is constant. (3) A curve whose tangent vector is constant is a straight line. So we have that a solution of the Burgers’ equation must verify
is constant. (3) A curve whose tangent vector is constant is a straight line. So we have that a solution of the Burgers’ equation must verify

And we call the family of curves given by 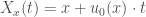 the characteristic curves of the solution.
the characteristic curves of the solution.
To extract more qualitative information about Burgers’ equation, let us take another spatial derivative of the equation, and call the function  . Then we have
. Then we have

So letting  be a characteristic curve, and write
be a characteristic curve, and write 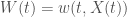 , we have that along the characteristic curve
, we have that along the characteristic curve
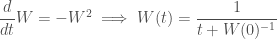
So in particular, we see that if  ,
, 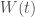 must blow up in time
must blow up in time  .
.
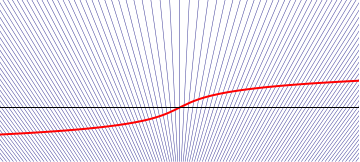 So what does this mean? We’ve seen that along characteristic lines, the value of
So what does this mean? We’ve seen that along characteristic lines, the value of  stays constant. But we’ve also seen that along those lines, the value of its spatial derivative can blow up if the initial slope is negative. Perhaps the best thing to do is to illustrate it with two pictures. In the pictures the thick, red curve is the initial velocity distribution
stays constant. But we’ve also seen that along those lines, the value of its spatial derivative can blow up if the initial slope is negative. Perhaps the best thing to do is to illustrate it with two pictures. In the pictures the thick, red curve is the initial velocity distribution 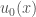 , shown with the black line representing the
, shown with the black line representing the  -axis: so when the curve is above the axis, initially the local fluid velocity is positive, and the fluid is moving to the right. The blue curves are the characteristic lines. In the first image to the right, we see that the initial velocity distribution is such that the velocity is increasing to the right. And so
-axis: so when the curve is above the axis, initially the local fluid velocity is positive, and the fluid is moving to the right. The blue curves are the characteristic lines. In the first image to the right, we see that the initial velocity distribution is such that the velocity is increasing to the right. And so  is always positive. We see that in this situation the flow is divergent, the flow lines getting further and further apart, corresponding to the solution where
is always positive. We see that in this situation the flow is divergent, the flow lines getting further and further apart, corresponding to the solution where 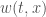 gets smaller and smaller along a flow line.
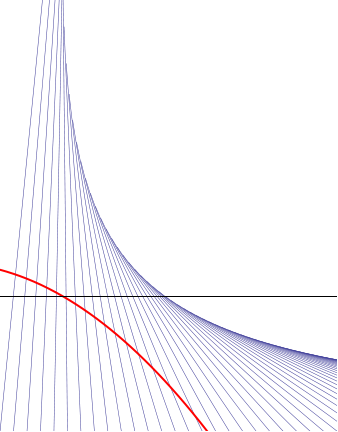
gets smaller and smaller along a flow line. 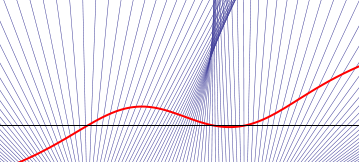 For the second image here on our left, the situation is different. The initial velocity distribution starts out increasing, then hits a maximum, dips down to a minimum, and finally increases again. In the regions where the velocity distribution is increasing, we see the same “spreading out” behaviour as before, with the flow lines getting further and further apart (especially in the upper left region). But for flowlines originating in the region where the velocity distribution is decreasing, those characteristic curves gets bunched together as time goes on, eventually intersecting! This intersection is what is known as a shock. From the picture, it becomes clear what the blow-up of
For the second image here on our left, the situation is different. The initial velocity distribution starts out increasing, then hits a maximum, dips down to a minimum, and finally increases again. In the regions where the velocity distribution is increasing, we see the same “spreading out” behaviour as before, with the flow lines getting further and further apart (especially in the upper left region). But for flowlines originating in the region where the velocity distribution is decreasing, those characteristic curves gets bunched together as time goes on, eventually intersecting! This intersection is what is known as a shock. From the picture, it becomes clear what the blow-up of 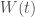 means: Suppose the initial velocity distribution is such that for two points
means: Suppose the initial velocity distribution is such that for two points 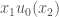 . Since the flow line originating from
. Since the flow line originating from 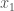 is moving faster, it will eventually catch up to the the flow line originating from
is moving faster, it will eventually catch up to the the flow line originating from  . When the two flow lines intersect, we have a problem: if we follow the flow line from
. When the two flow lines intersect, we have a problem: if we follow the flow line from 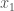 , the function
, the function  must take the value
must take the value 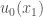 at the point; but if we follow the flow line from
at the point; but if we follow the flow line from  , the function must take the value
, the function must take the value 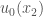 at the point. So we cannot consistently assign a value to the function
at the point. So we cannot consistently assign a value to the function  at the points of intersection for flow-lines in a way that satisfies Burgers’ equation.
at the points of intersection for flow-lines in a way that satisfies Burgers’ equation.
Another way of thinking about this difficulty is in terms of particle dynamics. Imagine the line being a highway, and points on it being cars. The dynamics of the traffic flow described by Burgers’ equation is one in which each driver starts at one speed (which can be in reverse), and maintains that speed completely without regard for the cars in front of or behind it. If we start out with a distribution where the leading cars always drive faster than the trailing ones, then the cars will spread further apart as time goes on. But if we start out with a distribution where a car in front is driving slower than a car behind, the second car will eventually catch up and crash into the one in front. And this is the formation of the shock wave.
(Now technically, in this view, once the two cars crash their flow-lines should end, and so cars that are in front of the collision and moving forward should not be affected by the collision at all. But if we imagine that instead of real cars, we are driving bumper cars, so after a collision, the car in front maintains speed at the velocity of the car that hit it, while the car in back drives at the velocity of the car it hit [so the they swap speeds in an elastic collision], then we have something like the picture plotted above.)
Shock boundary
Having established that shocks can form, we move on to the main discussion of this post: the geometry of the set of shock singularities. We will consider the purely local effects of the shocks; by which we mean that we will ignore the chain reactions as described in the parenthetical remark above. Therefore we will assume that at the formation of the shock, the flow-lines terminate and the particles they represent disappear. In other words, we will consider only shocks coming from nearest neighbor collisions. In this scenario, the time of existence of a characteristic line is precisely governed by the equation on  we derived before: that is given
we derived before: that is given 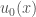 , the characteristic line emanating from
, the characteristic line emanating from  will run into the shock precisely at the time
will run into the shock precisely at the time 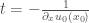 . (It will continue indefinitely in the future if the derivative is positive.)
. (It will continue indefinitely in the future if the derivative is positive.)
 The most well-known image of a shock formation is the image on the right, where we see the classic fan/wedge type shock. (Due to the simplicity in sketching thie diagram by hand, this is probably how most people are introduced to this type of diagrams, either on a homework set or in class.) What we see here is an illustration of the fact that
The most well-known image of a shock formation is the image on the right, where we see the classic fan/wedge type shock. (Due to the simplicity in sketching thie diagram by hand, this is probably how most people are introduced to this type of diagrams, either on a homework set or in class.) What we see here is an illustration of the fact that
If for 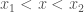 , we have
, we have  , and
, and  , then the shock boundary is degenerate: it consists of a single focal point.
, then the shock boundary is degenerate: it consists of a single focal point.
To see this analytically: observe that because the blow-up time depends on the first derivative of the initial velocity distribution, for such a set-up the blow-up time 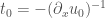 is constant for the various points. Then we see that the spatial coordinate of the blow-up will be
is constant for the various points. Then we see that the spatial coordinate of the blow-up will be 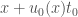 . But since
. But since 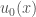 is linear in
is linear in  , we have
, we have
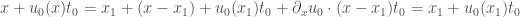
is constant. And therefore the shock boundary is degenerate.
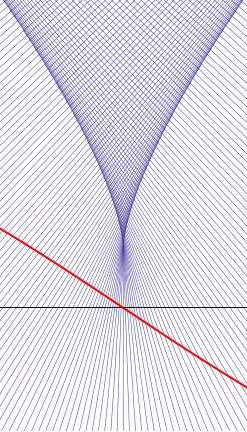
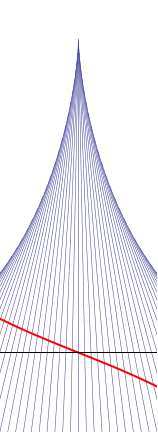
Next we consider the case where 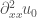 vanishes at some point
vanishes at some point  , but
, but 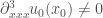 . The two pictures to the right of this paragraph illustrates the typical shock boundary behaviour. On the far right we have the slightly aphysical situation: notice that for a particle coming in from the left, before it hits its shock boundary, it first crosses the shock boundary formed by the particles coming in from the right. This is the situation where the third derivative is positive, and the cusp point which corresponds to the shock boundary for
. The two pictures to the right of this paragraph illustrates the typical shock boundary behaviour. On the far right we have the slightly aphysical situation: notice that for a particle coming in from the left, before it hits its shock boundary, it first crosses the shock boundary formed by the particles coming in from the right. This is the situation where the third derivative is positive, and the cusp point which corresponds to the shock boundary for  opens to the future. The nearer picture is the situation where the third derivative is negative, with the cusp point opening downwards. Notice that since we are in a neighborhood of a point where the second derivative vanishes, the initial velocity distributions both look almost straight, and it is hard to distinguish from this image the sign of the third derivative. The picture on the far right is based on an arctan type initial distribution, whereas the nearer picture is based on an
opens to the future. The nearer picture is the situation where the third derivative is negative, with the cusp point opening downwards. Notice that since we are in a neighborhood of a point where the second derivative vanishes, the initial velocity distributions both look almost straight, and it is hard to distinguish from this image the sign of the third derivative. The picture on the far right is based on an arctan type initial distribution, whereas the nearer picture is based on an 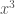 type initial distribution. Let us again analyse the situation more deeply. Near the point
type initial distribution. Let us again analyse the situation more deeply. Near the point  , we shall assume that
, we shall assume that 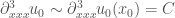 for some constant. And we will assume, using Galilean transformations, that
for some constant. And we will assume, using Galilean transformations, that 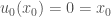 . Then letting
. Then letting 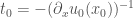 , we have
, we have
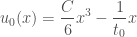
Thus as a function of  , the blow-up times of flow lines are given by
, the blow-up times of flow lines are given by

Solving for their blow-up profile 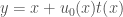 then gives (after quite a bit of algebraic manipulation)
then gives (after quite a bit of algebraic manipulation)
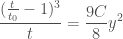
which can be easily seen to be a cusp: 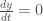 at
at 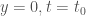 . And it is clear that the side the cusp opens is dependent on the sign of the third derivative,
. And it is clear that the side the cusp opens is dependent on the sign of the third derivative, 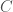 .
.
 The last bit of computation we will do is for the case
The last bit of computation we will do is for the case  . In this case we can take
. In this case we can take
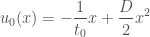
as an approximation. Then the blowup times will be
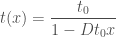
which leads to the blowup profile 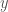 being [Thanks to Huy for the correction.]
being [Thanks to Huy for the correction.]
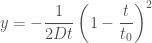
and a direct computation will then lead to the conclusion that in this generic scenario, the shock boundary will be everywhere tangent to the flow-line that ends there.
is the fundamental solution of the heat equation
is the number of spatial dimensions;
is the analogue of the radius of the ball, and in
, the point
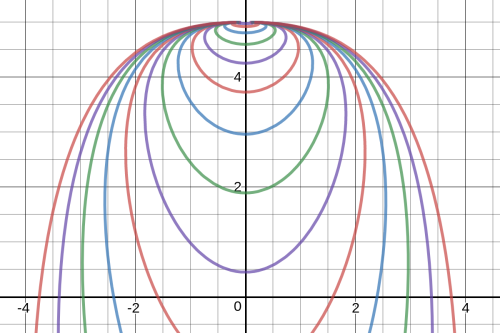
is the center. Below is a better visualization of the heat balls: the curves shown are the boundaries
in dimension
, for radii between 0.75 and 4 in steps of 0.25 (in particular all the red curves have integer radii). In higher dimensions the shape is generally the same, though they appear more “squashed” in the
direction.