differential/pseudo-Riemannian geometry | Bubbles Bad; Ripples Good

07/02/2013

Decay of Waves IV: Numerical Interlude

I offer two videos. In both videos the same colour scheme is used: we have four waves in red, green, blue, and magenta. The four represent the amplitudes of spherically symmetric free waves on four different types of spatial geometries: 1 dimension flat space, 2 dimensional flat space, 3 dimensional flat space, and a 3 dimensional asymptotically flat manifold with “trapping” (has closed geodesics). Can you tell which is which? (Answer below the fold.)

Read the rest of this entry »

30/09/2011

Gauge invariance, geometrically

A somewhat convoluted chain of events led me to think about the geometric description of partial differential equations. And a question I asked myself this morning was

Question
What is the meaning of gauge invariance in the jet-bundle treatment of partial differential equations?

The answer, actually, is quite simple.

Review of geometric formulation PDE
We consider here abstract PDEs formulated geometrically. All objects considered will be smooth. For more about the formal framework presented here, a good reference is H. Goldschmidt, “Integrability criteria for systems of nonlinear partial differential equations”, JDG (1967) 1:269–307.

A quick review: the background manifold $X$ is assumed (here we take a slightly more restrictive point of view) to be a connected smooth manifold. The configuration space $\mathcal{C}$ is defined to be a fibred manifold $p:\mathcal{C}\to X$ . By $J^r\mathcal{C}$ we refer to the fibred manifold of $r$ -jets of $\mathcal{C}$ , whose projection $p^r = \pi^r_0 \circ p$ where for $r > s$ we use $\pi^r_s: J^r\mathcal{C}\to J^s\mathcal{C}$ for the canonical projection.

A field is a (smooth) section $\phi \subset \Gamma \mathcal{C}$ . A simple example that capture most of the usual cases: if we are studying mappings between manifolds $\phi: X\to N$ , then we take $\mathcal{C} = N\times X$ the trivial fibre bundle. The $s$ -jet operator naturally sends $j^s: \Gamma\mathcal{C} \ni \phi \mapsto j^s\phi \in \Gamma J^r\mathcal{C}$ .

A partial differential equation of order $r$ is defined to be a fibred submanifold $J^r\mathcal{C} \supset R^r \to X$ . A field is said to solve the PDE if $j^r\phi \subset R^r$ .

In the usual case of systems of PDEs on Euclidean space, $X$ is taken to be $\mathbb{R}^d$ and $\mathcal{C} = \mathbb{R}^n\times X$ the trivial vector bundle. A system of $m$ PDEs of order $r$ is usually taken to be $F(x,\phi, \partial\phi, \partial^2\phi, \ldots, \partial^r\phi) = 0$ where

$\displaystyle F: X\times \mathbb{R}^n \times \mathbb{R}^{dn} \times \mathbb{R}^{\frac{1}{2}d(d+1)n} \times \cdots \times \mathbb{R}^{{d+r-1 \choose r} n} \to \mathbb{R}^m$

is some function. We note that the domain of $F$ can be identified in this case with $J^r\mathcal{C}$ , We can then extend $F$ to $\tilde{F}: J^r\mathcal{C} \ni c \mapsto (F(c),p^r(c)) \in \mathbb{R}^m\times X$ a fibre bundle morphism.

If we assume that $\tilde{F}$ has constant rank, then $\tilde{F}^{-1}(0)$ is a fibred submanifold of $J^r\mathcal{C}$ , and this is our differential equation.

Gauge invariance
In this frame work, the gauge invariance of a partial differential equation relative to certain symmetry groups can be captured by requiring $R^r$ be an invariant submanifold.

More precisely, we take

Definition
A symmetry/gauge group $\mathcal{G}$ is a subgroup of $\mathrm{Diff}(\mathcal{C})$ , with the property that for any $g\in\mathcal{G}$ , there exists a $g'\in \mathrm{Diff}(X)$ with $p\circ g = g' \circ p$ .

It is important we are looking at the diffeomorphism group for $\mathcal{C}$ , not $J^r\mathcal{C}$ . In general diffeomorphisms of $J^r\mathcal{C}$ will not preserve holonomy for sections of the form $j^r\phi$ , a condition that is essential for solving PDEs. The condition that the symmetry operation “commutes with projections” is to ensure that $g:\Gamma\mathcal{C}\to\Gamma\mathcal{C}$ , which in particular guarantees that $g$ extends to a diffeomorphism of $J^rC$ with itself that commutes with projections.

From this point of view, a (system of) partial differential equation(s) $R^r$ is said to be $\mathcal{G}$ -invariant if for every $g\in\mathcal{G}$ , we have $g(R^r) \subset R^r$ .

We give two examples showing that this description agrees with the classical notions.

Gauge theory. In classical gauged theories, the configuration space $\mathcal{C}$ is a fibre bundle with structure group $G$ which acts on the fibres. A section of $G\times X \to X$ induces a diffeomorphism of $\mathcal{C}$ by fibre-wise action. In fact, the gauge symmetry is a fibre bundle morphism (fixes the base points).

General relativity. In general relativity, the configuration space is the space of Lorentzian metrics. So the background manifold is the space-time $X$ . And the configuration space is the open submanifold of $S^2T^*X$ given by non-degenerate symmetric bilinear forms with signature (-+++). A diffeomorphism $\Psi:X\to X$ induces $T^*\Psi = (\Psi^{-1})^*: T^*X \to T^*X$ and hence a configuration space diffeomorphism that commutes with projection. It is in this sense that Einstein’s equations are diffeomorphism invariant.

Notice of course, this formulation does not contain the “physical” distinction between global and local gauge transformations. For example, for a linear PDE (so $\mathcal{C}$ is a vector bundle and $R^r$ is closed under linear operations), the trivial “global scaling” of a solution is considered in this frame work a gauge symmetry, though it is generally ignored in physics.

3 Comments

30/08/2011

Extensions of (co)vector fields to tangent bundles

I am reading Sasaki’s original paper on the construction of the Sasaki metric (a canonical Riemannian metric on the tangent bundle of a Riemannian manifold), and the following took me way too long to understand. So I’ll write it down in case I forgot in the future.

In section two of the paper, Sasaki consider “extended transformations and extended tensors”. Basically he wanted to give a way to “lift” tensor fields from a manifold to tensor fields of the same rank on its tangent bundle. And he did so in the language of coordinate changes, which geometrical content is a bit hard to parse. I’ll discuss his construction in a bit. But first I’ll talk about something different.

The trivial lifts
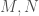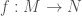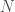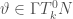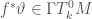Let $M, N$ be smooth manifolds, and let $f:M\to N$ a submersion. Then we can trivially lift covariant objects on $N$ to equivalent objects on $M$ by the pull-back operation. To define the pull-back, we start with a covariant tensor field $\vartheta \in \Gamma T^0_kN$ , and set $f^*\vartheta \in \Gamma T^0_kM$ by the formula:

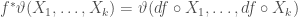
$\displaystyle f^*\vartheta(X_1,\ldots,X_k) = \vartheta(df\circ X_1, \ldots, df\circ X_k)$

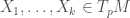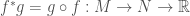where the $X_1, \ldots, X_k \in T_pM$ , and we use that $df(p): T_pM \to T_{f(p)}N$ . Observe that for a function $g: N \to \mathbb{R}$ , the pull-back is simply $f^*g = g\circ f :M\to N\to\mathbb{R}$ .

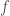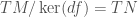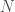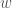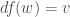On the other hand, for contravariant tensor fields, the pull-back is not uniquely defined: using that $f$ is a submersion, we have that $TM / \ker(df) = TN$ , so while, given a vector field $v$ on $N$ , we can always find a vector field $w$ on $M$ such that $df(w) = v$ , the vector field 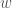$w$ is only unique up to an addition of a vector field that lies in the kernel of 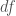$df$ . If, however, that $M$ is Riemannian, then we can take the orthogonal decomposition of $TM$ into the kernel and its complement, thereby getting a well-defined lift of the vector field (in other words, by exploiting the identification between the tangent and cotangent spaces).

Remarkably, the extensions defined by Sasaki is not this one.

(Let me just add a remark here: given two manifolds, once one obtain a well defined way of lifting vectors, covectors, and functions from one to the other, such that they are compatible ( $\vartheta^*(v^*) = [\vartheta(v)]^*$ ), one can extend this mapping to arbitrary tensor fields.)

The extensions defined by Sasaki
As seen above, if we just rely on the canonical submersion $\pi:TM\to M$ , we cannot generally extend vector fields. Sasaki’s construction, however, strongly exploits the fact that $TM$ is the tangent bundle of $M$ .

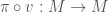We start by looking at the vector field extension defined by equation (2.6) of the linked paper. We first observe that a vector field $v$ on a manifold $M$ is a section of the tangent bundle. That is, $v$ is a map $M\to TM$ such that the composition with the canonical projection $\pi\circ v:M\to M$ is the identity map. This implies, using the chain rule, that the map $d(\pi\circ v)= d\pi \circ dv: TM\to TM$ is also the identity map. 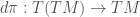Now, $d\pi: T(TM) \to TM$ is the projection induced by the projection map 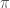$\pi$ , which is different from the canonical projection $\pi_2: T(TM) \to TM$ from the tangent bundle of a manifold to the manifold itself. 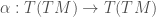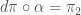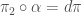However, a Proposition of Kobayashi (see “Theory of Connections” (1957), Proposition 1.4), shows that there exists an automorphism $\alpha:T(TM) \to T(TM)$ such that $d\pi \circ \alpha = \pi_2$ and $\pi_2\circ\alpha = d\pi$ . 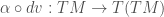So $v$ as a differential mapping induces a map $\alpha\circ dv: TM \to T(TM)$ , which is a map from the tangent bundle $TM$ to the double tangent bundle 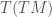$T(TM)$ , which when composed with the canonical projection 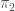$\pi_2$ is the identity. In other words, 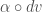$\alpha\circ dv$ is a vector field on $TM$ .

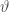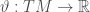Next we look at the definition (2.7) for one-forms. Give $\vartheta$ a one-form on $M$ , it induces naturally a scalar function on $TM$ : for $p\in M, v\in T_pM$ , we have $\vartheta: TM\to \mathbb{R}$ taking value $\vartheta(p)\cdot v$ . Hence its differential $d\vartheta$ is a one-form over $TM$ .

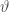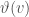Now, what about scalar functions? Let $\vartheta$ be a one-form and $v$ be a vector field on $M$ , we consider the pairing of their extensions to $TM$ . It is not too hard to check that the corresponding scalar field to $\vartheta(v)$ , when evaluated at 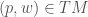$(p,w)\in TM$ , is in fact 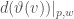$d(\vartheta(v))|_{p,w}$ , the derivative of the scalar function 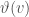$\vartheta(v)$ in the direction of 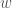$w$ at point 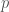$p$ . In general, the compatible lift of scalar fields 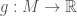$g:M\to \mathbb{R}$ to $TM$ is the function $\tilde{g}(p,v) = dg(p)[v]$ .

Using this we can extend the construction to arbitrary tensor fields, and a simple computation yields that this construction is in fact identical, for rank-2 tensors, to the expressions given in (2.8), (2.9), and (2.10) in the paper.

The second extension
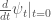The above extension is not the only map sending vectors on $M$ to vectors on $TM$ . In the statement of Lemmas 3 there is also another construction. Given a vector field $v$ , it induces a one parameter family of diffeomorphisms on $TM$ via that maps $\psi_t(p,w) = (p, w+vt)$ . Its differential $\frac{d}{dt}\psi_t|_{t=0}$ is a vector field over $TM$ .

The construction in the statement of Lemma 4 is the trivial one mentioned at the start of this post.

1 Comment

09/06/2011

Decay of waves IIIb: tails for homogeneous linear equation on curved background

Now we will actually show that the specific decay properties of the linear wave equation on Minkowski space–in particular the strong Huygens’ principle–is very strongly tied to the global geometry of that space-time. In particular, we’ll build, by hand, an example of a space-time where geometry itself induces back-scattering, and even linear, homogeneous waves will exhibit a tail.

For convenience, the space-time we construct will be spherically symmetric, and we will only consider spherically symmetric solutions of the wave equation on it. We will also focus on the 1+3 dimensional case. Read the rest of this entry »

28/01/2010

The “Hoop Conjecture” of Kip Thorne and Spherically Symmetric Space-times

Abstract. (This being a rather long post, I feel the need to write one.) In the post I first gather some miscellaneous thoughts on what the hoop conjecture is and why it is difficult to prove in general. After this motivation, I show also how the statement becomes much easier to state and prove in spherical symmetry: the entire argument collapses to an exercise in ordinary differential equations. In particular, I demonstrate a theorem that is analogous, yet slightly different, from a recent result of Markus Khuri, using much simpler machinery.

The Hoop conjecture is a proposed criterion for when a black-hole will form under gravitational collapse. Kip Thorne, in 1972 [see Thorne, Nonspherical Gravitational Collapse: a Short Review in Magic without Magic] made the conjecture that (I paraphrase here)

Horizons form when and only when a mass $M$ gets compacted into a region whose circumference $C$ in EVERY direction is bounded by $C \lesssim M$ .

This conjecture, now widely under the name of “Hoop conjecture”, is deliberately vague. (This seemed to have been the trend in physics, especially in general relativity. Conjectures are often stated in such a way that half the effort spent in proving said conjectures are used to find the correct formulation of the statement itself.) Read the rest of this entry »

1 Comment

01/07/2009

Straightedge and compass constructions

Classical Euclidean geometry is based on the familiar five postulates. The first two are equivalent to the assumption of the existence of a straightedge; the third gives the existence of a compass. The fourth essentially states that space is locally Euclidean, while the fifth, the infamous parallel postulate, assumes that space is globally Euclidean.

A quick digression: by now, most people are aware of the concept of non-Euclidean geometry as described by Bolyai and Lobachevsky, and independently by Gauss. These types of geometries make also the first four postulates. By simply abandoning the fifth postulate, we can arrive a geometries in which every pair of “lines” intersect (in other words, geometries in which “parallel lines” do not exist), or in which parallel lines are non-unique. (As a side note, one of the primary preoccupations of mathematicians is the existence-and-uniqueness of objects. With our obsession of classifying things, we ask often the question, “Does an object exist with properties X and Y?” and follow it up with, “Is there only one object that possesses properties X and Y?” One may have been subjected to this analysis as early as high school algebra when one is asked to classify whether a system of linear, algebraic equations have solutions, and whether the solution is a point or a line.) With even this relaxation, the space is still locally Euclidean (by the fourth postulate): a small portion of the surface will look “flat” when you blow it up (the same way how from our point of view, the Earth often looks flat). It is, however, possible to also relax the fourth postulate. The easiest example to imagine is by taking a piece of paper and rolling it up into a cone. At the vertex of the cone, going around one full turn is no longer going around 360 degrees. The “total angle” at the vertex will be smaller. So if we define a “right angle” as an angle that is exactly one quarter of the “total angle” at the point, the right angle at the vertex will be smaller! You can experiment with it yourself by drawing four rays from the vertex and then unfurling the piece of paper. Geometries with this kind of structures are often studied under the name of orbifolds.

In any case, let us return to the topic at hand.

Classical Euclidean geometry is filled with constructive proofs (the modern methods of mathematics–proof by contradiction, principle of strong induction, and existence proofs without construction–are only really popular after the 18th century). Read the rest of this entry »

2 Comments

	Willie Wong on TeXLive — on Androi…
	Aca on TeXLive — on Androi…
	Topology Preliminary… on Continuity of the infimum
	Willie Wong on Heat ball
	jack on Heat ball
	Willie Wong on In defense of integration by…
	Tom Copeland on In defense of integration by…

Category: differential/pseudo-Riemannian geometry