A prominent academic, who happens not to be a mathematician, visited my home institution recently and gave a public address about the role of the university in the modern world. Most of what he said concerning our teaching mission are the usual platitudes about not being stuck in the past and making sure that our curricular content and learning objectives are aligned with what we would expect a 21st century college graduates to need.
It however bugged me to no end that the recurring example this particular individual returns to for something old-fashioned and “ought not be taught” is integration by parts; and he justifies this by mentioning that computer algebra systems (or even just google) can do the integrals faster and better than we humans can.
I don’t generally mind others cracking jokes at mathematicians’ expense. But this particular self-serving strawman uttered by so well-regarded an individual is, to those of us actually in the field teaching calculus to freshmen and sophomores, very damaging and disingenuous.
I happened to have just spent the entirety of last year rethinking how we can best teach calculus to the modern engineering majors. Believe me, students nowadays know perfectly well when we are just asking them to do busywork; they also know perfectly well that computer algebra systems are generally better at finding closed-form integral expressions than we can. Part of the challenge of the redesign that I am involved in is precisely to convince the students that calculus is worth learning in spite of computers. The difficulty is not in dearth of reason; on the contrary, there are many good reasons why a solid grounding of calculus is important to a modern engineering students. To give a few examples:
- Taylor series are in fact important because of computers, since they provide a method of compactly encoding an entire function.
- Newton’s method for root finding (and its application to, say, numerical optimization) is build on a solid understanding of differential calculus.
- The entirety of the finite element method of numerical simulation, which underlies a lot of civil and mechanical engineering applications, are based on a variational formulation of differential equations that, guess what, only make sense when one understand integration by parts.
- The notion of Fourier transform which is behind a lot of signal/image processing requires understanding how trigonometric functions behave under integration.
No, the difficulty for me and my collaborator is narrowing down a list of examples that we can not only reasonably explain to undergraduate students, but also have them have some hands-on experience working with.
When my collaborator and I were first plunged into this adventure of designing engineering-specific calculus material, one of the very first things that we did was to seek out inputs from our engineering colleagues. My original impulse was to cut some curricular content in order to give the students a chance to develop deeper understanding of fewer topics. To that end I selected some number of topics which I thought are old-fashioned, out-dated, and no longer used in this day and age. How wrong I was! Even something like “integration by partial fractions” which most practicing mathematicians will defer to a computer to do has its advocates (those who have to teach control theory insists that a lot of fundamental examples in their field can be reduced to evaluating integrals of rational functions, and a good grasp of how such integrals behave is key to developing a general sense of how control theory works).
In short, unlike some individuals will have you believe, math education is not obsolete because we all have calculators. In fact, I would argue the opposite: math education is especially pertinent now that we all have calculators. Long gone was the age where a superficial understanding of mathematics in terms of its rote computations is a valuable skill. A successful scientist or engineer needs to be able to effectively leverage the large toolbox that is available to her, and this requires a much deeper understanding of mathematics, one that goes beyond just the how but also the what and the why.
There are indeed much that can be done to better math education for the modern student. But one thing that shouldn’t be done is getting rid of integration by parts.
is the fundamental solution of the heat equation
is the number of spatial dimensions;
is the analogue of the radius of the ball, and in
, the point
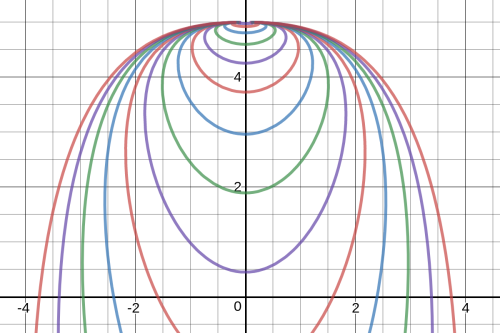
is the center. Below is a better visualization of the heat balls: the curves shown are the boundaries
in dimension
, for radii between 0.75 and 4 in steps of 0.25 (in particular all the red curves have integer radii). In higher dimensions the shape is generally the same, though they appear more “squashed” in the
direction.