(The following is somewhat rough and may have typos.)
Let us begin by setting the notations and recalling what happens without the Stieltjes part.
Defn (Partition)
Let 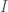 be a closed interval. A partition
be a closed interval. A partition 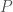 is a finite collection of closed subintervals
is a finite collection of closed subintervals 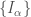 such that
such that
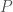 is finite;
is finite;
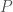 covers
covers 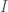 , i.e.
, i.e. 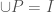 ;
;
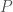 is pairwise almost disjoint, i.e. for
is pairwise almost disjoint, i.e. for  distinct elements of
distinct elements of 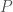 , their intersection contains at most one point.
, their intersection contains at most one point.
We write 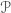 for the set of all partitions of
for the set of all partitions of 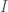 .
.
Defn (Refinement)
Fix 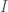 a closed interval, and
a closed interval, and 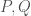 two partitions. We say that
two partitions. We say that 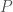 refines
refines 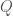 or that
or that 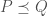 if for every
if for every  there exists
there exists 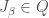 such that
such that 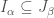 .
.
Defn (Selection)
Given 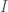 a closed interval and
a closed interval and 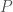 a partition, a selection
a partition, a selection  is a mapping that satisfies
is a mapping that satisfies 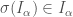 .
.
Defn (Size)
Given 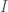 a closed interval and
a closed interval and 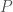 a partition, the size of
a partition, the size of 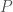 is defined as
is defined as  , where
, where 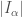 is the length of the closed interval
is the length of the closed interval 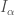 .
.
Remark In the above we have defined two different preorders on the set 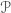 of all partitions. One is induced by the size: we say that
of all partitions. One is induced by the size: we say that  if
if  . The other is given by the refinement
. The other is given by the refinement 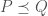 . Note that neither are partial orders. (But that the preorder given by refinement can be made into a partial order if we disallow zero-length degenerate closed intervals.) Note also that if
. Note that neither are partial orders. (But that the preorder given by refinement can be made into a partial order if we disallow zero-length degenerate closed intervals.) Note also that if 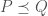 we must have
we must have  .
.
Now we can define the notions of integrability.
Defn (Integrability)
Let 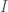 be a closed, bounded interval and
be a closed, bounded interval and 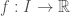 be a bounded function. We say that
be a bounded function. We say that 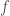 is integrable with integral
is integrable with integral  in the sense of
in the sense of
- Riemann if for every
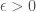 there exists
there exists 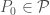 such that for every
such that for every 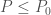 and every selection
and every selection  we have
we have
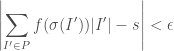
- Generalised-Riemann if for every
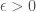 there exists
there exists 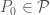 such that for every
such that for every  and every selection
and every selection 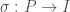 we have
we have
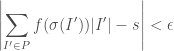
- Darboux if
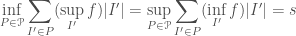
From the definition it is clear that “Riemann integrable” implies “Generalised-Riemann integrable”. Furthermore, we have clearly that for a fixed 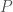
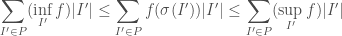
and that if 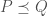 we have
we have
so “Darboux integrable” also implies “Generalised-Riemann integrable”. A little bit more work shows that “Generalised-Riemann integrable” also implies “Darboux integrable” (if the suprema and infima are obtained on the intervals  , this would follow immediately; using the boundedness of the intervals we can find
, this would follow immediately; using the boundedness of the intervals we can find  such that the Riemann sum approximates the upper or lower Darboux sums arbitrarily well.
such that the Riemann sum approximates the upper or lower Darboux sums arbitrarily well.
The interesting part is the following
Theorem
Darboux integrable functions are Riemann integrable. Thus all three notions are equivalent.
Proof. Let 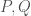 be partitions. Let
be partitions. Let  , and let
, and let 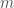 be the number of non-degenerate subintervals in
be the number of non-degenerate subintervals in 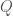 . We have the following estimate
. We have the following estimate
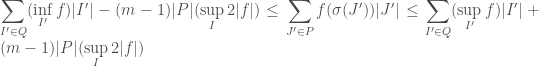
The estimate follows by noting that “most” of the 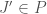 will be proper subsets of
will be proper subsets of 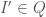 , and there can be at most
, and there can be at most 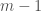 of the
of the  that straddles between two different non-degenerate sub-intervals of
that straddles between two different non-degenerate sub-intervals of 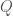 . To prove the theorem it suffices to choose first a
. To prove the theorem it suffices to choose first a 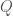 such that the upper and lower Darboux sums well-approximates the integral. Then we can conclude for all
such that the upper and lower Darboux sums well-approximates the integral. Then we can conclude for all 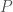 with
with 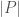 sufficiently small the Riemann sum is almost controlled by the
sufficiently small the Riemann sum is almost controlled by the 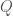 -Darboux sums. Q.E.D.
-Darboux sums. Q.E.D.
Now that we have recalled the case of the usual integrability. Let us consider the case of the Stieltjes integrals: instead of integrating against 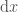 , we integrate against
, we integrate against 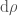 , where
, where  is roughly speaking a “cumulative distribution function”: we assume that
is roughly speaking a “cumulative distribution function”: we assume that  is a bounded monotonically increasing function.
is a bounded monotonically increasing function.
The definition of the integrals are largely the same, except that at every step we replace the width of the interval 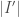 by the diameter of
by the diameter of 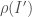 , i.e.
, i.e.  . The arguments above immediately also imply that
. The arguments above immediately also imply that
- “Riemann-Stieltjes integrable” implies “Generalised-Riemann-Stieltjes integrable”
- “Darboux-Stieltjes integrable” implies “Generalised-Riemann-Stieltjes integrable”
- “Generalised-Riemann-Stieltjes integrable” implies “Darboux-Stientjes integrable”
However, Darboux-Stieltjes integrable functions need not be Riemann-Stieltjes integrable. The possibility of failure can be seen in the proof of the theorem above, where we used the fact that 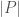 is allow to be made arbitrarily small. The same estimate, in the case of the Stieltjes version of the integrals, has
is allow to be made arbitrarily small. The same estimate, in the case of the Stieltjes version of the integrals, has 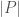 replaced by
replaced by 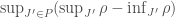 , which for arbitrary partitions need to shrink to zero. To have a concrete illustration, we give the following:
, which for arbitrary partitions need to shrink to zero. To have a concrete illustration, we give the following:
Example
Let ![I = [0,1]](https://s0.wp.com/latex.php?latex=I+%3D+%5B0%2C1%5D&bg=fff&fg=444444&s=0&c=20201002) . Let
. Let  if
if  and
and 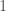 otherwise. Let
otherwise. Let  if
if  and
and 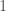 otherwise. Let
otherwise. Let  be the partition
be the partition ![\{ [0,\frac12], [\frac12,1]\}](https://s0.wp.com/latex.php?latex=%5C%7B+%5B0%2C%5Cfrac12%5D%2C+%5B%5Cfrac12%2C1%5D%5C%7D&bg=fff&fg=444444&s=0&c=20201002) . We have that
. We have that
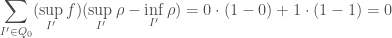
while
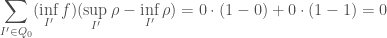
so we have that in particular the pair  is Darboux-Stieltjes integrable with integral 0. However, let
is Darboux-Stieltjes integrable with integral 0. However, let 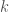 be any odd integer, consider the partition
be any odd integer, consider the partition  of
of ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=fff&fg=444444&s=0&c=20201002) into
into 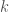 equal portions. Depending on the choice of the selection
equal portions. Depending on the choice of the selection 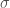 , we see that the sum can take the values
, we see that the sum can take the values
![\displaystyle \sum_{I'\in P_k} f(\sigma(I')) (\sup_{I'} \rho - \inf_{I'}\rho) = f(\sigma([\frac12 - \frac1{2k},\frac12 + \frac1{2k}])) (1 - 0) \in \{0,1\}](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5Csum_%7BI%27%5Cin+P_k%7D+f%28%5Csigma%28I%27%29%29+%28%5Csup_%7BI%27%7D+%5Crho+-+%5Cinf_%7BI%27%7D%5Crho%29+%3D+f%28%5Csigma%28%5B%5Cfrac12+-+%5Cfrac1%7B2k%7D%2C%5Cfrac12+%2B+%5Cfrac1%7B2k%7D%5D%29%29+%281+-+0%29+%5Cin+%5C%7B0%2C1%5C%7D&bg=fff&fg=444444&s=0&c=20201002)
which shows that the Riemann-Stieltjes condition can never be satisfied.
The example above where both 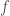 and
and  are discontinuous at the same point is essentially sharp. A easy modification of the previous theorem shows that
are discontinuous at the same point is essentially sharp. A easy modification of the previous theorem shows that
Prop
If at least one of 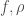 is continuous, then Darboux-Stieltjes integrability is equivalent to Riemann-Stieltjes integrability.
is continuous, then Darboux-Stieltjes integrability is equivalent to Riemann-Stieltjes integrability.
Remark The nonexistence of Riemann-Stieltjes integral when 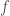 and
and  has shared discontinuity points is similar in spirit to the idea in distribution theory where whether the product of two distributions is well-defined (as a distribution) depends on their wave-front sets.
has shared discontinuity points is similar in spirit to the idea in distribution theory where whether the product of two distributions is well-defined (as a distribution) depends on their wave-front sets.