Just realised (two seeks ago, but only gotten around to finish this blog posting now) that an argument used to prove a proposition in a project I am working on is wrong. After reducing the problem to its core I found that it is something quite elementary. So today’s post would be of a different flavour from the ones of recent past.
Question Let 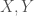 be topological spaces. Let
be topological spaces. Let 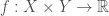 be a bounded, continuous function. Is the function
be a bounded, continuous function. Is the function 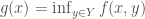 continuous?
continuous?
Intuitively, one may be tempted to say “yes”. Indeed, there are plenty of examples where the answer is in the positive. The simplest one is when we can replace the infimum with the minimum:
Example Let the space 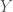 be a finite set with the discrete topology. Then
be a finite set with the discrete topology. Then 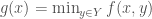 is continuous.
is continuous.
Proof left as exercise.
But in fact, the answer to the question is “No”. Here’s a counterexample:
Example Let 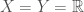 with the standard topology. Define
with the standard topology. Define
![\displaystyle f(x,y) = \begin{cases} 1 & x > 0 \\ 0 & x < -e^{y} \\ 1 + x e^{-y} & x\in [-e^{y},0] \end{cases}](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+f%28x%2Cy%29+%3D+%5Cbegin%7Bcases%7D+1+%26+x+%3E+0+%5C%5C+0+%26+x+%3C+-e%5E%7By%7D+%5C%5C+1+%2B+x+e%5E%7B-y%7D+%26+x%5Cin+%5B-e%5E%7By%7D%2C0%5D++%5Cend%7Bcases%7D&bg=fff&fg=444444&s=0&c=20201002)
which is clearly continuous. But the infimum function  is roughly the Heaviside function:
is roughly the Heaviside function: 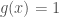 if
if  , and
, and 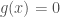 if
if 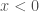 .
.
So what is it about the first example that makes the argument work? What is the different between the minimum and the infimum? A naive guess maybe that in the finite case, we are taking a minimum, and therefore the infimum is attained. This guess is not unreasonable: there are a lot of arguments in analysis where when the infimum can be assumed to be attained, the problem becomes a lot easier (when we are then allowed to deal with a minimizer instead of a minimizing sequence). But sadly that is not (entirely) the case here: for every  , we can certainly find a
, we can certainly find a 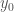 such that
such that  . So attaining the infimum point-wise is not enough.
. So attaining the infimum point-wise is not enough.
What we need, here, is compactness. In fact, we have the following
Theorem If 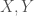 are topological spaces and
are topological spaces and 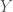 is compact. Then for any continuous
is compact. Then for any continuous 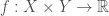 , the function
, the function 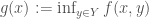 is well-defined and continuous.
is well-defined and continuous.
Proof usually proceeds in three parts. That  follows from the fact that for any fixed
follows from the fact that for any fixed  ,
,  is a continuous function defined on a compact space, and hence is bounded (in fact the infimum is attained). Then using that the sets
is a continuous function defined on a compact space, and hence is bounded (in fact the infimum is attained). Then using that the sets  and
and  form a subbase for the topology of
form a subbase for the topology of 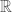 , it suffices to check that
, it suffices to check that  and
and 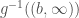 are open.
are open.
Let 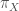 be the canonical projection
be the canonical projection 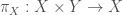 , which we recall is continuous and open. It is easy to see that
, which we recall is continuous and open. It is easy to see that 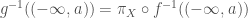 . So continuity of
. So continuity of 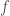 implies that this set is open. (Note that this part does not depend on compactness of
implies that this set is open. (Note that this part does not depend on compactness of 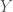 . In fact, a minor modification of this proof shows that for any family of upper semicontinuous functions
. In fact, a minor modification of this proof shows that for any family of upper semicontinuous functions 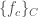 , the pointwise infimum
, the pointwise infimum 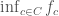 is also upper semicontinuous, a fact that is very useful in convex analysis. And indeed, the counterexample function given above is upper semicontinuous.)
is also upper semicontinuous, a fact that is very useful in convex analysis. And indeed, the counterexample function given above is upper semicontinuous.)
It is in this last part, showing that 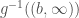 is open, that compactness is crucially used. Observe that
is open, that compactness is crucially used. Observe that 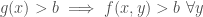 . In other words
. In other words  an open set. This in particular implies that
an open set. This in particular implies that  there exists a “box” neighborhood
there exists a “box” neighborhood 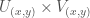 contained in
contained in 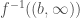 . Now using compactness of
. Now using compactness of 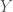 , a finite subset
, a finite subset 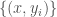 of all these boxes cover
of all these boxes cover 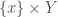 . And in particular we have
. And in particular we have

and hence 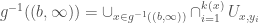 is open. Q.E.D.
is open. Q.E.D.
One question we may ask is how sharp is the requirement that 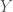 is compact. As with most things in topology, counterexamples abound.
is compact. As with most things in topology, counterexamples abound.
Example Let 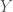 be any uncountably infinite set equipped with the co-countable topology. That is, the collection of open subsets are precisely the empty set and all subsets whose complement is countable. The two interesting properties of this topology are (a)
be any uncountably infinite set equipped with the co-countable topology. That is, the collection of open subsets are precisely the empty set and all subsets whose complement is countable. The two interesting properties of this topology are (a) 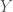 is not compact and (b)
is not compact and (b) 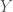 is hyperconnected. (a) is easy to see: let
is hyperconnected. (a) is easy to see: let 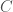 be some countably infinite subset of
be some countably infinite subset of 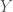 . For each
. For each  let
let 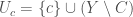 . This forms an open cover with not finite sub-cover. Hyperconnected spaces are, roughly speaking, spaces in which all open nonempty sets are “large”, in the sense that they mutually overlap a lot. In particular, a continuous map from a hyperconnected space to a Hausdorff space must be constant. In our case we can see this directly: suppose
. This forms an open cover with not finite sub-cover. Hyperconnected spaces are, roughly speaking, spaces in which all open nonempty sets are “large”, in the sense that they mutually overlap a lot. In particular, a continuous map from a hyperconnected space to a Hausdorff space must be constant. In our case we can see this directly: suppose  is a continuous map. Fix
is a continuous map. Fix 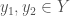 . Let
. Let  be open neighborhoods of
be open neighborhoods of 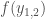 . Since
. Since 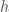 is continuous,
is continuous, 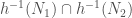 is open and non-empty (by the co-countable assumption). Therefore
is open and non-empty (by the co-countable assumption). Therefore 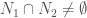 for any pairs of neighborhoods. Since
for any pairs of neighborhoods. Since 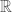 is Hausdorff, this forces
is Hausdorff, this forces 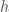 to be the constant map. This implies that for any topological space
to be the constant map. This implies that for any topological space  , a continuous function
, a continuous function 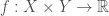 is constant along
is constant along 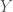 , and hence for any
, and hence for any 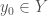 , we have
, we have 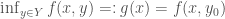 is continuous.
is continuous.
One can try to introduce various regularity/separation assumptions on the spaces 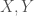 to see at what level compactness becomes a crucial requirement. As an analyst, however, I really only care about topological manifolds. In which case the second counterexample up top can be readily used. We can slightly weaken the assumptions and still prove the following partial converse in essentially the same way.
to see at what level compactness becomes a crucial requirement. As an analyst, however, I really only care about topological manifolds. In which case the second counterexample up top can be readily used. We can slightly weaken the assumptions and still prove the following partial converse in essentially the same way.
Theorem Let  be Tychonoff, connected, and first countable, such that
be Tychonoff, connected, and first countable, such that  contains a non-trivial open subset whose closure is not the entire space; and let
contains a non-trivial open subset whose closure is not the entire space; and let 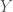 be paracompact, Lindelof. Then if
be paracompact, Lindelof. Then if 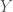 is noncompact, there exists a continuous function
is noncompact, there exists a continuous function 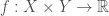 such that
such that 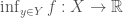 is not continuous.
is not continuous.
Remark Connected (nontrivial) topological manifolds automatically satisfy the conditions on  and
and 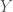 except for non-compactness. The conditions given are not necessary for the theorem to hold; but they more or less capture the topological properties used in the construction of the second counterexample above.
except for non-compactness. The conditions given are not necessary for the theorem to hold; but they more or less capture the topological properties used in the construction of the second counterexample above.
Remark If  is such that every open set’s closure is the entire space, we must have that it is hyperconnected (let
is such that every open set’s closure is the entire space, we must have that it is hyperconnected (let 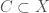 be a closed set. Suppose
be a closed set. Suppose  is another closed set such that
is another closed set such that  . Then
. Then 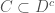 and vice versa, but
and vice versa, but  is open, so
is open, so  . Hence
. Hence  cannot be written as the union of two proper closed subsets). And if it is Tychonoff, then
cannot be written as the union of two proper closed subsets). And if it is Tychonoff, then  is either the empty-set or the one-point set.
is either the empty-set or the one-point set.
Lemma For a paracompact Lindelof space that is noncompact, there exists a countably infinite open cover 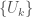 and a sequence of points
and a sequence of points  such that
such that  if
if 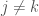 .
.
Proof: By noncompactness, there exists an open cover that is infinite. By Lindelof, this open cover can be assumed to be countable, which we enumerate by 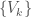 and assume WLOG that
and assume WLOG that  . Define
. Define 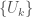 and
and  inductively by:
inductively by: 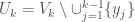 and choose
and choose 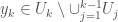 .
.
Proof of theorem: We first construct a sequence of continuous functions on  . Let
. Let 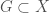 be a non-empty open set such that its closure-complement
be a non-empty open set such that its closure-complement 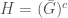 is a non-empty open set (
is a non-empty open set ( exists by assumption). By connectedness
exists by assumption). By connectedness  , so we can pick
, so we can pick  in the intersection. Let
in the intersection. Let 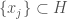 be a sequence of points converging to
be a sequence of points converging to  , which exists by first countability. Using Tychonoff, we can get a sequence of continuous functions
, which exists by first countability. Using Tychonoff, we can get a sequence of continuous functions  on
on  such that
such that 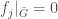 and
and 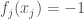 .
.
On 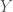 , choose an open cover
, choose an open cover 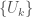 and points
and points  per the previous Lemma. By paracompactness we have a partition of unity
per the previous Lemma. By paracompactness we have a partition of unity 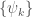 subordinate to
subordinate to 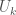 , and by the conclusion of the Lemma we have that
, and by the conclusion of the Lemma we have that 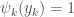 . Now we define the function
. Now we define the function

which is continuous, and such that 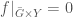 . But by construction
. But by construction 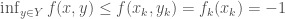 , which combined with the fact that
, which combined with the fact that  shows the desired result. q.e.d.
shows the desired result. q.e.d.
is the fundamental solution of the heat equation
is the number of spatial dimensions;
is the analogue of the radius of the ball, and in
, the point
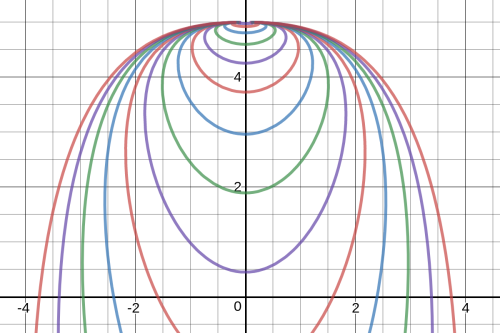
is the center. Below is a better visualization of the heat balls: the curves shown are the boundaries
in dimension
, for radii between 0.75 and 4 in steps of 0.25 (in particular all the red curves have integer radii). In higher dimensions the shape is generally the same, though they appear more “squashed” in the
direction.