Decay of Waves IV: Numerical Interlude

I offer two videos. In both videos the same colour scheme is used: we have four waves in red, green, blue, and magenta. The four represent the amplitudes of spherically symmetric free waves on four different types of spatial geometries: 1 dimension flat space, 2 dimensional flat space, 3 dimensional flat space, and a 3 dimensional asymptotically flat manifold with “trapping” (has closed geodesics). Can you tell which is which? (Answer below the fold.)

Decay of waves IIIb: tails for homogeneous linear equation on curved background

Now we will actually show that the specific decay properties of the linear wave equation on Minkowski space–in particular the strong Huygens’ principle–is very strongly tied to the global geometry of that space-time. In particular, we’ll build, by hand, an example of a space-time where geometry itself induces back-scattering, and even linear, homogeneous waves will exhibit a tail.

For convenience, the space-time we construct will be spherically symmetric, and we will only consider spherically symmetric solutions of the wave equation on it. We will also focus on the 1+3 dimensional case.

Decay of waves IIIa: nonlinear tails in Minkowski space redux

Before we move on to the geometric case, I want to flesh out the nonlinear case mentioned in the end of the last post a bit more. Recall that it was shown for generic nonlinear (actually semilinear; for quasilinear and worse equations we cannot use Duhamel’s principle) wave equations, if we put in compact support for the initial data, we expect the first iterate to exhibit a tail. One may ask whether it is possible that, in fact, this is an artifact of the successive approximation scheme; that in fact somehow it always transpires that a conspiracy happens, and all the higher order iterates cancel out the tail coming from the first iterate. This is rather unlikely, owing to the fact that the convergence to is dominated by a geometric series. But to just make double sure, here we give a nonlinear system of wave equations such that the successive approximation scheme converges after finitely many steps (in fact, after the first iterate), and so we can also explicitly compute the rate of decay for the nonlinear tail. While the decay rate is not claimed to be generic (though it is), the existence of one such example with a fixed decay rate shows that for a statement quantifying over all nonlinear wave equations, it would be impossible to demonstrate better decay rate than the one exhibited.

Decay of waves IIb: Minkowski space, with right-hand side

In the first half of this second part of the series, we considered solutions to the linear, homogeneous wave equation on flat Minkowski space, and showed that for compactly supported initial data, we have strong Huygens’ principle. We further made references to the fact that this behaviour is expected to be unstable. In this post, we will further illustrate this instability by looking at Equation 1 first with a fixed source , and then with a nonlinearity .

Duhamel’s Principle

To study how one can incorporate inhomogeneous terms into a linear equation, and to get a qualitative grasp of how the source term contributes to the solution, we need to discuss the abstract method known as Duhamel’s Principle. We start by illustrating this for a very simple ordinary differential equation.

Consider the ODE satisfied by a scalar function :

Equation 13

when , we can easily solve the equation with integration factors

Using this as a sort of an ansatz, we can solve the inhomogeneous equation as follows. For convenience we denote by the anti-derivative of . Then multiplying Equation 13 through by , we have that

Equation 14

which we solve by integrating

Equation 15

If we write , then we can rewrite Equation 15 as given by an integral operator

Equation 15′

Decay of waves IIa: Minkowski background, homogeneous case

Now let us get into the mathematics. The wave equations that we will consider take the form

Equation 1

where is a real valued function defined on (1+n)-dimensional Minkowski space that describes our solution, and represents a “source” term. When vanishes identically, we say that we are looking at the linear, homogeneous wave equation. When is itself a function of and its first derivatives, we say that the equation is a semilinear wave equation.

We first start with the homogeneous, linear case.

Homogeneous wave equation in one spatial dimension

One interesting aspect of the wave equation is that it only possesses the second, multidimensional, dispersive mechanism as described in my previous post. In physical parlance, the “phase velocity” and the “group velocity” of the wave equation are the same. And therefore, a solution of the wave equation, quite unlike a solution of the Schroedinger equation, will not exhibit decay when there is only one spatial dimension (mathematically this is one significant difference between relativistic and quantum mechanics). In this section we make a computation to demonstrate this, a fact that would also be useful later on when we look at higher (in particular, three) dimensions.

Use for the variable representing spatial position. The wave equation can be written as

Now we perform a change of variables: let and be the canonical null variables. The change of variable formula replaces

Equation 2

and we get that in the coordinate system,

Equation 3

Decay of waves I: Introduction

In the next week or so, I will compose a series of posts on the heuristics for the decay of the solutions of the wave equation on curved (and flat) backgrounds. (I have my fingers crossed that this does not end up aborted like my series of posts on compactness.) In this first post I will give some physical intuition of why waves decay. In the next post I will write about the case of linear and nonlinear waves on flat space-time, which will be used to motivate the construction, in post number three, of an example space-time which gives an upper bound on the best decay that can be generally expected for linear waves on non-flat backgrounds. This last argument, due to Mihalis Dafermos, shows that why the heuristics known as Price’s Law is as good as one can reasonably hope for in the linear case. (In the nonlinear case, things immediately get much much worse as we will see already in the next post.)

This first post will not be too heavily mathematical, indeed, the only realy foray into mathematics will be in the appendix; the next ones, however, requires some basic familiarity with partial differential equations and pseudo-Riemannian geometry.

Minimal blow-up solution to an inhomogeneous NLS

Yesterday I went to a wonderful talk by Jeremie Szeftel on his recent joint work with Pierre Raphaël. The starting point is the following equation:

Eq 1. Homogeneous NLS
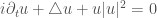on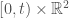

It is known as the mass-critical nonlinear Schrödinger equation. One of its very interesting properties is that it admits a soliton solution 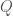, which is the unique positive (real) radial solution to

Eq 2. Soliton equation

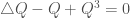
Plugging 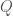into the homogeneous NLS, we see that it evolves purely by phase-rotation: it represents a non-dispersing standing wave. Physically, this represents the case when the self-interaction attractive non-linearity exactly balances out the tendency for a wave to disperse.

As one can easily see from its form, the homogeneous NLS has a large class of continuous symmetries:

• Time translation
• Spatial translation
• Phase translation (translation in Fourier space)
• Dilation
• Galilean boosts

(It is also symmetric under rotations, but as the spatial rotation group is compact, it cannot cause problems for the analysis [a lesson from concentration compactness; I’ll write about this another time], so we’ll just forget about it for the time being.) The NLS also admits the so-called pseudo-conformal transformation, which is a discrete 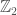action that replacing

Eq 3. Pseudo-conformal inversion

maps a solution to another solution. A particularly interesting phenomenon related to this additional symmetry is the existence of the minimal mass blow-up solution: by acting on 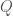(the soliton) with the pseudo-conformal transform, we obtain a solution that blows-up in finite time. But why do we call this a “minimal mass” solution? This is because previously it has been shown by Michael Weinstein (I think) that for any initial data to the NLS with initial mass ( 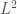norm) smaller than that of 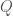, the solution must exists for all time, whereas for any values of mass strictly above that of 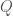, one can find a (in fact, multiple) solution that blows-up in finite time. With concentration compactness methods, Frank Merle was able to show that the pseudo-conformally inverted 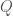is the only initial data that leads to finite-time blow-up with that fixed mass.

In some sense, however, the homogeneous NLS is too-nice of a equation: because of its astounding number of symmetries, one can write down an explicit, self-similar blow-up solution just via the pseudo-conformal transform. A natural question to ask is that whether the property of the existence/uniqueness of a minimal mass blow-up solution can exist for more generic looking equations. The toy model one is led to consider is

Eq 4. Inhomogeneous NLS

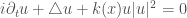
for which the case reduces to the homogeneous equation. The addition of the arbitrary term kills all of the symmetries except phase translation and time translation. The former is a trivial set of symmetries (whose orbit is compact, so not posing any difficulty), while the latter is important since it generates the conservation of energy for this equation.

In the case where 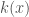is a differentiable, bounded function, some facts about this equation are known through the work of Merle. Without loss of generality, we will assume from now on that 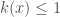(we can always arrange for this by rescaling the equation). It was found that in this case, if the initial mass of the data is smaller than that of 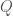, again, we have global existence of a solution. Heuristically, the idea is that 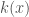measures the self-interaction strength of the particle, which can vary with its spatial position: the larger the value of 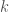, the more strongly the interaction. Now, in the homogeneous case the low-mass initial data does not have enough matter to lead to a strong enough self-interaction, so the dispersive behavior dominates and there cannot be concentration of energy and blow-up. Heuristically we expect that for interactions strictly weaker than the homogeneous case (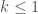), the dispersion should still dominate over the attractive self-force.

Furthermore, Merle also found that a minimal mass blow-up to the inhomogeneous NLS can only occur if (hits an interior maximum) at some finite point, and that 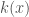is bounded strictly away from 1 outside some large compact set. In this case, the blow-up can only occur in such a way that leads to a concentration of energy at the maximum point. Heuristically, again, this is natural: the strong self-interaction gives a lower potential energy. So it is natural to expect the particle to slide down into this potential well when it concentrates. If the potential asymptotes to the minimum at infinity, however, one may expect the wave to slide out to infinity and disperse, so it is important to have a strict maximum of the interaction strength in the interior.

Szeftel and Raphaël’s work show that such a blow-up solution indeed exists, and is in fact unique.

Around the local maximum of 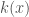, we can (heuristically) expand by Taylor polynomials. That is a local maximum implies that we have schematically

In the case where the Hessian term vanishes, by “zooming in” along a pre-supposed self-similar blow-up with rates identical to the one induced by the pseudo-conformal transform in the homogeneous case, we can convince ourselves that the more we zoom in, the flatter 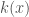looks. In this case, then it is not too unreasonable that the focusing behavior of the homogeneous case carries over: by zooming in sufficiently we rapidly approach a situation which is locally identical to the homogeneous case. If the energy is already concentrating, then the errors introduced at “large distances” will be small and controllable. This suggest that the problem admits a purely perturbative treatment. This, indeed, was the case, as Banica, Carles, and Duyckaerts have shown.

On the other hand, of the Hessian term does not vanish, one sees that it remains scale-invariant down to the smallest scales. In other words, no matter how far we zoom in, the pinnacle at 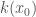will always look curved. In this situation, a perturbative method is less suitable, and this is the regime where Szeftel and Raphaël works.

The trick, it seems to me, is the following (I don’t think I completely understand all the intricacies of the proof; here I’ll just talk about the impression I got from the talk and from looking a bit at the paper): it turns out that by inverting the pseudo-conformal transform, we can reformulate the blow-up equation as a large-time equation in some rescaled variables, where now the potential 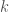depends on the scaling parameter which also depends on time. The idea is to “solve backwards from infinity”. If we just plug-in naïvely the stationary solution 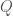at infinity, there will be error terms when we evolve back. What we want to do is capture the error terms. If we directly linearize the equation around 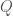, we will pick-up negative-eigenmodes, which will lead to exponential blow-up and destroy our ansatz. To overcome this difficulty, as is standard, the authors applied modulation theory. The idea behind modulation theory is that all the bad eigenmodes for the linearized equation of a good Hamiltonian system should be captured by the natural symmetries. In this case, we don’t have any natural symmetries to use. But we have “almost” symmetries coming from the homogeneous system. So we consider the manifold of functions spanned by symmetry transformations of 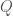, and decompose the solution as a projection part which lives on the manifold, and an orthogonal part 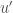. In this way, all the wild, uncontrolled directions of the flow are captured in some sort of motion on the symmetry manifold. We don’t actually particularly care how the flow happens, as the flow on the manifold preserves norms. The only bit we care about the flow is how it converges as time approaches the blow-up time: this is what gives us the blow-up rate of the equation.

As it turns out, this decomposition is a very good one: the analysis showed that the flow on the manifold is a good approximation (to the fourth order) of the actual physical flow. This means that the orthogonal error 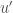is going to be rather small and controllable. Of course, to establish these estimates is a lot of hard work; fundamentally, however, the idea is a beautiful one.