Decay of Waves IV: Numerical Interlude

I offer two videos. In both videos the same colour scheme is used: we have four waves in red, green, blue, and magenta. The four represent the amplitudes of spherically symmetric free waves on four different types of spatial geometries: 1 dimension flat space, 2 dimensional flat space, 3 dimensional flat space, and a 3 dimensional asymptotically flat manifold with “trapping” (has closed geodesics). Can you tell which is which? (Answer below the fold.)

“The asymptotically hyperboloidal is not asymptotically null.”

By way of Roland Donninger, I learned today of the statement above which is apparently well-known in the numerical relativity community.

It may seem intuitively surprising: after all, the archetype of an asymptotically hyperboloidal surface is the hyperboloid as embedded in Minkowski space. Let be the spherical coordinate system for the Minkowski space , the hyperboloid embeds in it as the surface . If you draw a picture we see clearly that the surface is asymptotic to the null cone …

The key, however, lies in the definition. For better or for worse, the definition under which the titular statement makes sense the following:

Definition
Let be an asymptotically simple space-time (or one for which one can define a Penrose compactification), and let be the compactified space-time. We say that a hypersurface is asymptotically null if the transversely and the tangent space of is null along .

Now suppose near we can foliate via a double-null foliation , with . Let be a coordinate on so that form a coordinate system for a neighborhood of . Assume that our surface can be written as a graph

where is a function. Then the asymptotically null condition is just that . Taking a Taylor expansion we have that this means

.

For the usual conformal compactification of Minkowski space, we have . Hence we require that an asymptotically null surface to have convergence to the null surface at rate (if is sufficiently differentiable; if we relax the differentiability at infinity we see that the above condition allows us to relax all the way to , but is not admissible).

On the other hand, the hyperboloid is given by and so is not asymptotically null. And indeed, we can also check by direct computation that in the usual conformal compactification of Minkowski space, the limit of the hyperboloid at null infinity is space-like.

Gauge invariance, geometrically

A somewhat convoluted chain of events led me to think about the geometric description of partial differential equations. And a question I asked myself this morning was

Question
What is the meaning of gauge invariance in the jet-bundle treatment of partial differential equations?

The answer, actually, is quite simple.

Review of geometric formulation PDE
We consider here abstract PDEs formulated geometrically. All objects considered will be smooth. For more about the formal framework presented here, a good reference is H. Goldschmidt, “Integrability criteria for systems of nonlinear partial differential equations”, JDG (1967) 1:269–307.

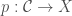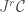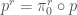A quick review: the background manifold is assumed (here we take a slightly more restrictive point of view) to be a connected smooth manifold. The configuration space is defined to be a fibred manifold . By we refer to the fibred manifold of -jets of , whose projection where for 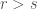we use for the canonical projection.

A field is a (smooth) section 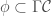. A simple example that capture most of the usual cases: if we are studying mappings between manifolds 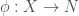, then we take 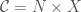the trivial fibre bundle. The -jet operator naturally sends .

A partial differential equation of order is defined to be a fibred submanifold 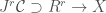. A field is said to solve the PDE if .

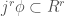In the usual case of systems of PDEs on Euclidean space, is taken to be 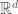and 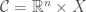the trivial vector bundle. A system of 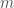PDEs of order is usually taken to be where

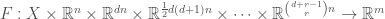
is some function. We note that the domain of 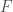can be identified in this case with 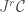, We can then extend 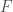to 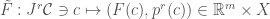a fibre bundle morphism.

If we assume that 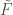has constant rank, then is a fibred submanifold of 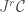, and this is our differential equation.

Gauge invariance
In this frame work, the gauge invariance of a partial differential equation relative to certain symmetry groups can be captured by requiring 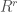be an invariant submanifold.

More precisely, we take

Definition
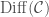A symmetry/gauge group is a subgroup of , with the property that for any 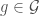, there exists a 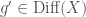with .

It is important we are looking at the diffeomorphism group for , not 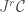. In general diffeomorphisms of 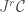will not preserve holonomy for sections of the form 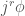, a condition that is essential for solving PDEs. The condition that the symmetry operation “commutes with projections” is to ensure that , which in particular guarantees that extends to a diffeomorphism of 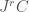with itself that commutes with projections.

From this point of view, a (system of) partial differential equation(s) 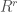is said to be -invariant if for every 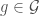, we have .

We give two examples showing that this description agrees with the classical notions.

Gauge theory. In classical gauged theories, the configuration space is a fibre bundle with structure group which acts on the fibres. A section of induces a diffeomorphism of by fibre-wise action. In fact, the gauge symmetry is a fibre bundle morphism (fixes the base points).

General relativity. In general relativity, the configuration space is the space of Lorentzian metrics. So the background manifold is the space-time . And the configuration space is the open submanifold of given by non-degenerate symmetric bilinear forms with signature (-+++). A diffeomorphism induces 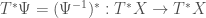and hence a configuration space diffeomorphism that commutes with projection. It is in this sense that Einstein’s equations are diffeomorphism invariant.

Notice of course, this formulation does not contain the “physical” distinction between global and local gauge transformations. For example, for a linear PDE (so is a vector bundle and 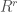is closed under linear operations), the trivial “global scaling” of a solution is considered in this frame work a gauge symmetry, though it is generally ignored in physics.

Decay of waves IIIb: tails for homogeneous linear equation on curved background

Now we will actually show that the specific decay properties of the linear wave equation on Minkowski space–in particular the strong Huygens’ principle–is very strongly tied to the global geometry of that space-time. In particular, we’ll build, by hand, an example of a space-time where geometry itself induces back-scattering, and even linear, homogeneous waves will exhibit a tail.

For convenience, the space-time we construct will be spherically symmetric, and we will only consider spherically symmetric solutions of the wave equation on it. We will also focus on the 1+3 dimensional case.

Decay of waves I: Introduction

In the next week or so, I will compose a series of posts on the heuristics for the decay of the solutions of the wave equation on curved (and flat) backgrounds. (I have my fingers crossed that this does not end up aborted like my series of posts on compactness.) In this first post I will give some physical intuition of why waves decay. In the next post I will write about the case of linear and nonlinear waves on flat space-time, which will be used to motivate the construction, in post number three, of an example space-time which gives an upper bound on the best decay that can be generally expected for linear waves on non-flat backgrounds. This last argument, due to Mihalis Dafermos, shows that why the heuristics known as Price’s Law is as good as one can reasonably hope for in the linear case. (In the nonlinear case, things immediately get much much worse as we will see already in the next post.)

This first post will not be too heavily mathematical, indeed, the only realy foray into mathematics will be in the appendix; the next ones, however, requires some basic familiarity with partial differential equations and pseudo-Riemannian geometry.

The “Hoop Conjecture” of Kip Thorne and Spherically Symmetric Space-times

Abstract. (This being a rather long post, I feel the need to write one.) In the post I first gather some miscellaneous thoughts on what the hoop conjecture is and why it is difficult to prove in general. After this motivation, I show also how the statement becomes much easier to state and prove in spherical symmetry: the entire argument collapses to an exercise in ordinary differential equations. In particular, I demonstrate a theorem that is analogous, yet slightly different, from a recent result of Markus Khuri, using much simpler machinery.

The Hoop conjecture is a proposed criterion for when a black-hole will form under gravitational collapse. Kip Thorne, in 1972 [see Thorne, Nonspherical Gravitational Collapse: a Short Review in Magic without Magic] made the conjecture that (I paraphrase here)

Horizons form when and only when a mass gets compacted into a region whose circumference in EVERY direction is bounded by .

This conjecture, now widely under the name of “Hoop conjecture”, is deliberately vague. (This seemed to have been the trend in physics, especially in general relativity. Conjectures are often stated in such a way that half the effort spent in proving said conjectures are used to find the correct formulation of the statement itself.)

“No Hair” theorems

Hum, now I am a bit confused. I doubt any “prominent mathematician” will read this blog and comment, so I guess I’ll ask them in person next time I go to a conference.

The question is about the term “no hair theorem”.